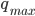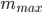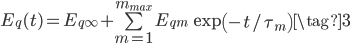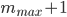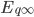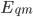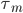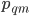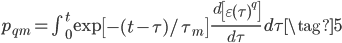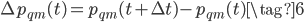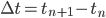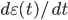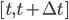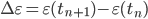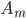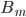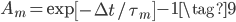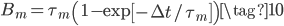A nonlinear constitutive equation based on the modified superposition method has been implemented in a user material subroutine (UMAT) for Abaqus unidimensional applications. A Python application that generates the Fortran subroutine, based on the number of terms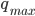 
and 
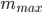employed in the formulation, can be downloaded here.
Requirements: Python
How to use it:
- Download the Python subroutine a href="http://sposs.org/software/umat_nlv_1d/abaqus_umat_nlv_beam_v2.py">here.
- Edit the file to change the parameters qmax and mmax according to your material fitting.
- Execute the command "python abaqus_umat_nlv_beam"
Thats it. Your material subroutine is ready to use with Abaqus.
A brief theoretical description on the nonlinear viscoelastic constitutive equation employed in the implementation is presented below.
Theoretical description
For the nonlinear viscoelastic behavior, many investigations have been based on the multiple integral representation due to Green and Rivlin. Several approximate methods have been proposed to simplify the multiple integral representations. The modified superposition method proposed by Findley is implemented here. One can verifiy that this leads to the following relations:
The tensile stress relaxation function may be described by the following Prony series,
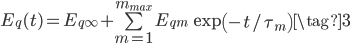
with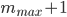 
terms. 
, 
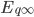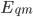and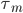 
are the material parameters. The hereditary integral may be re-written as,
where the state variables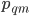 
are described by,
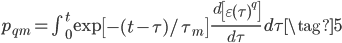
The state variable increment is given by,
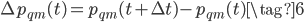
being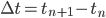 
the time step increment. Replacing Eq. \eqref{eq:eq5} in the first term to the right of Eq. \eqref{eq:eq6} and considering 
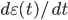constant over the interval 
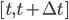the following approximation is obtained,
\begin{equation}
\begin{gathered}
{p_{qm}}(t + \Delta t) = \exp \left[ { - \Delta t/{\tau _m}} \right]{p_{qm}}(t) + \int_{{\kern 1pt} t}^{{\kern 1pt} t + \Delta t} {\exp \left[ { - (t + \Delta t - \tau )/{\tau _m}} \right]{\mkern 1mu} \left( {\frac{{{\mkern 1mu} d[\varepsilon {{(\tau )}^q}]}}{{d\tau }}} \right){\mkern 1mu} d\tau } \\
\approx \exp \left[ { - \Delta t/{\tau _m}} \right]{p_{qm}}(t) + \left( {\frac{{{\mkern 1mu} \Delta {\varepsilon ^q}}}{{\Delta t}}} \right){\mkern 1mu} {\tau _m}{\mkern 1mu} \left( {1 - \exp \left[ { - \Delta t/{\tau _m}} \right]} \right) \\
\end{gathered}
\label{eq:eq7}\tag{7}\
\end{equation}
Different approximation algorithms are described by Sorvari and Hamalainen. Replacing Eq. \eqref{eq:eq7} into \eqref{eq:eq6} leads to,
\begin{equation}
\Delta {p_{qm}} \approx {p_{qm}}{\mkern 1mu} {A_m} + \left( {\frac{{{\mkern 1mu} \Delta {\varepsilon ^q}}}{{\Delta t}}} \right){\mkern 1mu} {B_m}
\label{eq:eq8}\tag{8}
\end{equation}
where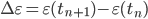 
is the strain increment 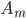and 
and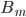 
are described by,
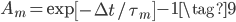
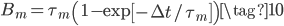
The derivative of the state variable increment in relation to the strain increment is given by,
\begin{equation}
\frac{{\partial \Delta {p_{qm}}}}{{\partial \Delta \varepsilon }} = q{\mkern 1mu} {\left( {\varepsilon + \Delta \varepsilon } \right)^{q - 1}}\frac{{{B_m}}}{{\Delta t}}
\label{eq:eq11}\tag{11}
\end{equation}
The stress increment can be obtained using Eq. \eqref{eq:eq4},
\begin{equation}
\Delta \sigma = {\mkern 1mu} \sum\limits_{q = 1}^{{q_{max}}} {\left\{ {{E_{q\infty }}{\mkern 1mu} \Delta {\varepsilon ^q} + {\mkern 1mu} \left( {\sum\limits_{m = 1}^{{m_{max}}} {{E_{qm}}\Delta {p_{qm}}} } \right)} \right\}}
\label{eq:eq12}\tag{12}
\end{equation}
The material Jacobian matrix is then obtained deriving Eq. \eqref{eq:eq12} with respect to the strain increment. By replacing Eq. \eqref{eq:eq11} into the resultant equation, the following relation is obtained,
\begin{equation}
\frac{{\partial \Delta \sigma }}{{\partial \Delta \varepsilon }} = {\mkern 1mu} \sum\limits_{q = 1}^{{q_{max}}} {\left\{ {{E_{q\infty }}{\mkern 1mu} q{\mkern 1mu} {{\left( {\varepsilon + \Delta \varepsilon } \right)}^{q - 1}} + {\mkern 1mu} \left( {\sum\limits_{m = 1}^{{m_{max}}} {{E_{qm}}{\mkern 1mu} q{\mkern 1mu} {\mkern 1mu} {{\left( {\varepsilon + \Delta \varepsilon } \right)}^{q - 1}}\frac{{{B_m}}}{{\Delta t}}{\mkern 1mu} {\mkern 1mu} } } \right)} \right\}}
\label{eq:eq13}\tag{13}
\end{equation}
which is used for numerical implementation into the finite element package user subroutine.
******************************************************************************
Revision Notes:
1.0 - Initial version
2.0 - Nonlinear strain increment corrected
******************************************************************************
Author : Marcelo Caire
Copyright : <2015> <INOCEANO>
