 |
PyFlex
1.0
Riser cross section analysis
|
 |
PyFlex
1.0
Riser cross section analysis
|
This is a program for generating stresses in the cross section of flexible risers. Input is time histories of pressure tensions and curvatures together with cross sectional properties.
All files can be found on bitbucket. Clone the repository, make sure you have python and the nescessary packages installed. Thereafter, run main.py
To generate the documentation locally, download doxygen and run it using the DoxyFile under docs/Doxygen in the repository.
To find details of the theory, one can explore the source code itself, or the source code documentation. A brief description is also given here.
The solution method is a two step procedure, where the axisymmetric response is found first and the response from bending and frictional response is found subsequently based on contact pressures between the layers found when solving the axisymmetric system. The following assumptions are made:
The figure below shows the global coordinate system, the meaning of \( \theta \) and the corner numbering.
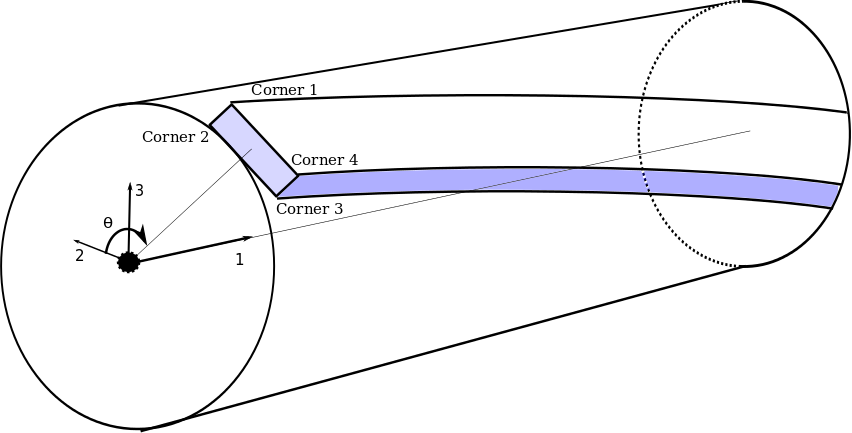
A positive \(\kappa_i\) is defined as a curvature that gives axial tension for a point with a positiv value along the \(i\) axis.
The radiuses and thicknesses are indicated in the following figure.
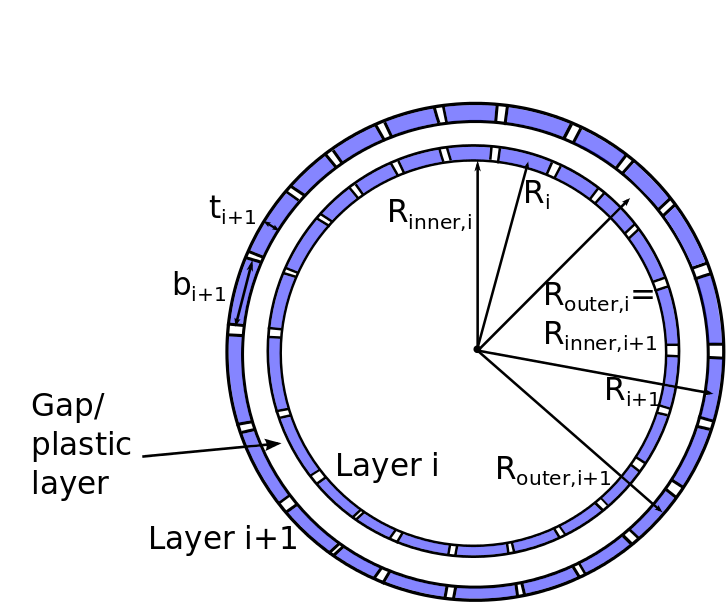
The main results from the axisymmetric analysis is stresses and contact pressures between layers. The axisymmetric algorithm allows for the modelling of plastic sheaths and also takes possible gap formation between the layers into account.
In order to do this a system of equations with constraints on them needs to be solved. PyFlex solves 3 equations for each helic layer, 2 for each sheath layer and one equation for each layer interface taken to be in contact. In addition we solve one equation for overall axial equilibrium. The equations for the wire layers are to a large extent based on the equations found in MARINTEK/NTNU/4Subsea (2014), while the equations for the sheath layers are based on expressions found in Custodio e Vaz (2002). The equations are developed based on no pressure working in the hoop direction on the wire layers. This is not a correct assumption for the carcass, or in a case with flooded annulus, but is thought to not give rise to significant errors in fatigue calculations.
The system is built in axisymmetric.systemsetup, and its governing equations are shown here:
\begin{align} \epsilon_{11} R_i -\epsilon_a cos(\alpha) R_i-sin^2(\alpha) u_3 = 0 \end{align}
Equilibrium of radial forces:
For wire layer:
\begin{align} \frac{E_i A_i n_i \epsilon _{11,i} \sec \left(\alpha _i\right) sin^2\left(\alpha _i\right)}{r_i}-\frac{A_i \nu _i n_i p_i \sec \left(\alpha _i\right) sin^2\left(\alpha _i\right)}{2 f_f r_i}-\frac{A_i \nu _i n_i p_{i+1} \sec \left(\alpha _i\right) sin^2\left(\alpha _i\right)}{2 f_f r_i}-2 \pi p_i r_i+2 \pi p_{i+1} r_{i+1}+\pi r_i t_i+\pi r_{i+1} t_{i+1}=0 \end{align}
For sheath layer:
\begin{align} {1 \over E_i R_i (r^2_{int,i} - r^2_{out,i}} (p_{i+1} (1+\nu_i)(R^2_i(-1+2\nu_i)-r_{int,i}^2) r_{out,i}^2 - p_{i}(1+\nu_i)(R^2_i(-1+2\nu_i)-r_{out,i}^2)r_{int,i}^2)+ E_i R_i (r_{int,i}^2 - r_{out,i}^2) (u_{3,i} + R_i \nu_i \epsilon_{11,i})) =0 \end{align}
Thickness equilibrium:
For wire layer:
\begin{align} {\Delta t_i \over t_i} - {(1 + \nu^2_i)p_i \over 2 E_i f_f} - {(1 + \nu^2_i)p_{i+1} \over 2 E_i f_f} + \nu_i \epsilon_{11,i} = 0 \end{align}
For sheath layer:
\begin{align} \Delta t_i - {t_i \over E_i} ({(p_{i+1}-p_i) r_{int,i}^2 r_{out,i}^2\over R_i^2(r_{out,i}^2-r_{int,i}^2)} + {p_i r_{int,i}^2-p_{i+1}r_{out,i}^2 \over r_{out,i}^2 - r_{int,i}^2} - \nu_i (- { (p_{i+1}-p_i) r_{int,i}^2 r_{out,i}^2 \over R_i^2(r_{out,i}^2-r_{int,i}^2)} + {p_i r_{int,i}^2-p_{i+1}r_{out,i}^2 \over r_{out,i}^2 - r_{int,i}^2}) - {\nu_i \over r_{int,i}^2 - r_{out,i}^2} (-2 p_i \nu_i r_{int,i}^2+2 p_{i+1} \nu_i r_{out,i}^2 + E_i (r_{int,i}^2-r_{out,i}^2) \epsilon_{11,i} ) ) = 0 \end{align}
\begin{align} u_{3,i}-u_{3,i-1}-\frac{\Delta t_{i-1}}{2}-\frac{\Delta t_i}{2}+gap_i^{ini}=0 \end{align}
\begin{align} \sum_{i=0}^{n_{wirelayers}} ( E_i A_i n_i \epsilon _{11,i} \cos \left(\alpha _i\right)-\frac{A_i \nu _i n_i p_i \cos \left(\alpha _i \right)}{2 f_f}-\frac{A_i \nu _i n_i p_{i+1} \cos \left(\alpha _i\right)}{2 f_f}) + \sum_{i=0}^{n_{sheathlayers}} (A E_i \epsilon_{11,i}+\frac{2 A \nu _i p_i r_{in,i}^2}{r_{out,i}^2-r_{in,i}^2}-\frac{2 A \nu _i p_{i+1} r_{out,i}^2}{r_{out,i}^2-r_{int,i}^2}) = -\pi p_{ext} r_{ext}^2+\pi p_{int} r_{int}^2+T \end{align}
Solving the above equations directly applying the interface equation for all interfaces will give the correct results given that no gaps are present within the structure, however if gaps are present the interface equation should be removed and a known pressure of 0 should be applied instead on the interface. Several solutions are proposed for finding the correct solution. Skeie et al. (2012) proposes solving the constraints reformulating the equations as a quadratic programming (QP) problem. Due to Pythons preference for solving vectorized systems, the assumption that gaps are not often present and the fact that the stiffness matrix is constant for a given set of gaps, another solution was chosen here. First PyFlex solves the system for all instances in time assuming no gaps are present. Thereafter it checks for negative contact pressures. If negative contact pressures are found it finds all possible combinations of gaps based on the results, and consecutively solves the resulting equation system for the time steps where gaps are present, starting from the solutions with the most gaps between layers. It continues through the possible solutions until all time steps have a valid solution.
The bending stress from bending of wires can be calculated using two different options. Either by the equations presented by Sævik (1992) or Witz and Tan(1992). The equations by Sævik included in Pyflex is resulting from the assumption that the wires follows the loxodromic curve, thus only experiencing axial displacements. The equations for the bending stress coefficient about the strong and weak axis per curvature is:
\begin{align} bc_2 = (1+sin^2(\alpha))\cos(\alpha)\sin(\theta_{rel})|\kappa| \end{align}
\begin{align} bc_3 = -cos^4(\alpha)\cos(\theta_{rel})|\kappa| \end{align}
While they according to Witz and Tan is:
\begin{align} bc_2 = \cos(\theta_{rel})|\kappa| \end{align}
\begin{align} bc_3 = -\sin(\theta_{rel})\cos(\alpha)|\kappa| \end{align}
These coefficients are multiplied with the distance to the corner following the coordinate system indicated in Coordinate system and definitions and the Young's modulus to end up with the total bending stress.
As a flexible pipe is subjected to a curvature, shear forces builds up between the layers. When the curvatures are sufficiently small the available friction is large enough to withstand and sliding, while sliding occurs when the the shear force is larger than the available friction. In the stick domain the stresses arising from friction is found by assuming that the beam behaves as a Euler-Bernoulli beam and that plane sections remain plane, leading to a sinusoidal stress distribution around the beam. For helical members the stress is found as:
\begin{align} \sigma_{11,stick} = E_iR_i\cos^2(\alpha_i)\kappa\sin(\theta) \end{align}
giving a maximum of:
\begin{align} \sigma_{11,stick,max} = E_iR_i\cos^2(\alpha_i)\kappa \end{align}
The axial force in the wire is then:
\begin{align} F_{11} = E_iA_iR_i\cos^2(\alpha_i)\kappa \end{align}
In the full slip domain the maximum shear force is already built up between the layers and further bending does not introduce further stress. With the assumption that the contact pressure from the axisymmetric analysis still holds, the pressure distribution would be linear in this case, with the frictional stresses remaining at zero at the neutral axis.
The shear force does not build up uniformly, but builds up faster towards the neutral axis of the bending, leading to slip being initiated sooner here than away from the neutral axis. Also, the stress distribution is linear on the part of the cross section in slip, while remaining sinusoidal in the part where slip has not occured yet. In PyFlex the entire layer slips at the same time. To ensure conservatism, the distribution is kept at being sinusoidal and the curvature at which slip is initiated is assumed to be at the point where the stress from the plane sections remain plane assumption coincides with the maximum possible frictional stress.
The maximum frictional stress can be found from multiplying the available frictional shear force with the tendon length from the neutral axis to the top of the riser:
\begin{align} A_i\sigma_{fric,max,i} = b_i(p_i\mu_i+p_{i-1}\mu_{i-1})\frac{\pi R_i}{2|\sin(\alpha_i)|} \rightarrow \sigma_{stick,max,i} = b_i(p_i\mu_i+p_{i-1}\mu_{i-1})\frac{\pi R_i}{2|\sin(\alpha_i)|A_i} \end{align}
by equating the maximum available friction force with the force resulting from stick one can find an effective critical curvature as:
\begin{align} \kappa=b_i(p_i\mu_i+p_{i-1}\mu_{i-1})\frac{\pi}{2|\sin(\alpha_i)|E_iA_i\cos^2(\alpha_i)}=(p_i\mu_i+p_{i-1}\mu_{i-1})\frac{\pi}{2|\sin(\alpha_i)|E_it_i\cos^2(\alpha)} \end{align}
With the assumptions above in mind, the slipping of the wires will lead to a friction stress free configuration which is not straight. To go from a state were slip is initiated through a reversal to have full slip in the other direction, twice the effective curvature needs to be applied. Together with the assumption that the layer goes abruptly from stick to slip this means an elastic-perfectly plastic material model is suitable. As the shape of the stress distribution around the cross section is kept constant and the whole layer goes from stick to slip at once, the same material model can be used for all points around the cross section. The yield surface has a constant radius of the effective critical curvature and the and maximum frictional stress in curvature and stress space respectively. The model keeps track and updates the position of the yield surface to keep the material state within or on the border of the yield surface.
In this section aspects of using PyFlex will be described. As the source code is open, you can of course apply PyFlex as a library and apply it to your workflow as suitable. In this document however, the use through the GUI will be described.
An example of an inputfile can be seen in Example Inputfiles. The input file consists of key words and values. The values are seperated from the key words by one or more tabs. For key words where more than one value is to be given, they are to be divided by a comma. To group values, for example when describing tendon geometries, each group is divided by a comma, while each value within a group is seperated by one or more blank spaces, as exemplified below: LayerGeometry 1e-3 218.7e-3, 1e-3 45.3e-3, 5e-3 12e-3, 5e-3 12e-3 describing four layer geometries.
The text following # is parsed as a comment.
| Key word | Description |
|---|---|
| LayerRadii | The radii of the layers. Counting from the inenr layer. For now only helical layers are included in the model |
| LayerGeometry | hThe geometry of the tendons. Rectangular geometry assumed. For nonrectangular layers the resulting stresses will not be correct. However, applying the correct area will make the contact pressure calculation, as the only geometrical quantity that goes into it is the area of the tendon. |
| LayAngle | The lay angle of the layer. In the input file it is given in degrees, within the program it is given in radians. |
| CompNumber | Number of tendons in a layers |
| FrictionFactor | Friction factor on the inside of each layer. If only one is applied it is assumed to be valid for all layers. |
| YoungsModulus | The Youngs for all layers. |
| TypicalCurvature | Typical curvature of the cross section. An option for quickly verifying whether friction will contribute significantly to fatigue. |
| TypicalTension | Typical tension of the cross section. An option for quickly verifying whether friction will contribute significantly to fatigue. |
The keywords are case insensitive.
Input files are opened through the Open option under the File menu or by using the ctrl+o shortcut. The extension for the input files is dat.
The riser model is held in a tree view on the left, where the numbers can be manipulated. If more layers is needed, right click on 'Model data' and select 'Add layer'.
The time history file is in the current version an ASCII file containing the time, tension, curvatures and pressures. By default the sequence is as follows:
\(Time\) \(\kappa_2\) \(\kappa_3\) \(p_i\) \(p_e\)
As for the input file # is a comment character. If placed on the start of a line that line will be seen as a comment line. To change the sequence of input, add '# #' to the first line followed by the sequence of the data. The key words for the input quanteties are included in the Example Time History File. The time history files have the extension tim.
The time history files can be imported either one by one or by folder. If a folder is chosen, all *.tim files in that folder will be loaded into PyFlex.
The time series can be vizualized be right clicking the time series and select 'Plot the time histories'.
The full analysis is chosen by right clicking on the 'Calculations' item in the tree model in the left in the user interface. A tab containing the needed input and a space for dropping time history files will pop up on the lower right side of the GUI. In the current version the user is confined to choose analytical as the analysis method. Further the user can choose the following:
To include time series for analysis, drag and drop files from the tree model on the left side onto the calculation tab. For imported folder, one can drag and drop all time history files by clicking the 'Time histories from directory' item and dropping it.
When the analysis is run, the results pops up in a tab in the upper right window. The results are presented in a tree model. By clicking on an item, it is toggled on and off in the plot area to the right. The color of the font changes to match the color of the corresponding curve in the plot.
Exporting the results can be done in two ways. Under the tree model there is a button for exporting all results. This will create a hdf5 file containing all results and also the input time histories. The other way of exporting results is thorugh the tool bar on the plot. Through this the plotted results can be exported. It can be exported in ASCII format of hdf5 format. The ASCII file will have the extension ts.
Nugteren (2015) made a similar model to this, and carried out comparison of the results with results obtained by an unknown industry renowned software for the axisymmetric loads, and with the DNVGL software Helica for bending loads. The files used for this comparison is a part of this software. In the thesis the axisymmetric and bending models are called A and B respectively, the same naming is kept here.
In the axisymmetric model the quantities of interest is the axial stress in the layers themselves, and the contact pressures, as these influence the bending behavior.
The model has the following properties:
| Property | Layer 1 | Layer 2 | Layer 3 | Layer 4 | unit |
|---|---|---|---|---|---|
| Layer radii | 108.1 | 113 | 118.2 | 124.6 | mm |
| Layer thickness | 4 | 4 | 5 | 5 | mm |
| Layer width | 54.675 | 11.325 | 12 | 12 | mm |
| Lay angle | -86.1 | 87.6 | -30 | 30 | degrees |
| Number of tendons | 2 | 2 | 50 | 53 | - |
| Young's Modulus | 200 | 200 | 200 | 200 | MPa |
| Initial gap | - | 0.0 | 0.0 | 0.0 | mm |
The thickness of the two inner layers they are estimated from the difference in radius for the layers, while the width is adjusted to give the same area as in Nugterens thesis.
The definition of the five load cases were:
| Name | \( p_i \) | \(t_{eff}\) |
|---|---|---|
| LC1 | 462 bar | 0 kN |
| LC2 | 462 bar | 220.6 kN |
| LC3 | 0 bar | 220.6 kN |
| LC4 | 508 bar | 131.1 kN |
| LC5 | 721 bar | 0 kN |
Where the inner pressure is applied on the innermost layer. In the following table the axial stress in each layer is compared with both the unknown industrially accepted tool and the program of Nugteren.
| LC1 | LC2 | LC3 | LC4 | LC5 | |
|---|---|---|---|---|---|
| Layer 1 | |||||
| Design [MPa] | 347 | 338 | -9 | 376 | 542 |
| Nugteren [MPA] | 345 | 337 | -9 | 375 | 540 |
| Pyflex [MPA] | 349 | 342 | -8 | 379 | 545 |
| Deviation design [%] | 0.6 | 1.1 | -16.0 | 0.9 | 0.5 |
| Deviation Nugteren [%] | 1.2 | 1.4 | -16.0 | 1.2 | 0.9 |
| Layer 2 | |||||
| Design [MPa] | 329 | 321 | -8 | 357 | 514 |
| Nugteren [MPA] | 330 | 323 | -8 | 358 | 516 |
| Pyflex [MPA] | 334 | 327 | -7 | 363 | 521 |
| Deviation design [%] | 1.4 | 1.8 | -11.6 | 1.6 | 1.3 |
| Deviation Nugteren [%] | 1.1 | 1.1 | -11.6 | 1.3 | 0.9 |
| Layer 3 | |||||
| Design [MPa] | 314 | 359 | 45 | 372 | 490 |
| Nugteren [MPA] | 316 | 357 | 42 | 372 | 494 |
| Pyflex [MPA] | 309 | 351 | 42 | 365 | 483 |
| Deviation design [%] | -1.4 | -2.2 | -7.3 | -1.9 | -1.4 |
| Deviation Nugteren [%] | -2.1 | -1.6 | -0.7 | -1.9 | -2.2 |
| Layer 4 | |||||
| Design [MPa] | 229 | 271 | 42 | 277 | 357 |
| Nugteren [MPA] | 311 | 353 | 40 | 368 | 487 |
| Pyflex [MPA] | 303 | 345 | 41 | 358 | 473 |
| Deviation design [%] | 32.3 | 27.1 | -1.3 | 29.2 | 32.5 |
| Deviation Nugteren [%] | -2.5 | -2.4 | 3.6 | -2.7 | -2.9 |
The deviation deviates from what would have been reached by comparing the values in the table as more significant digits were applied for the results from PyFlex than what is shown in the table. Barring the results for the outermost layer, the layer stresses are similar. For the outermost layer on the other hand, the stresses from Nugterens model and PyFlex are comparable, but are seen to overestimate the stresses compared to the unknown design tool. As the solution method in this tool is not known speculation of why the significant differences arises are hard, however it underlines a need for more open test data.
The table below compares the obtained contact pressures.
| LC1 | LC2 | LC3 | LC4 | LC5 | |
|---|---|---|---|---|---|
| Layer 1 - Layer 2 | |||||
| Design [MPa] | 14.70 | 15.33 | 0.64 | 16.54 | 22.95 |
| Nugteren [MPA] | 14.99 | 15.59 | 0.62 | 16.84 | 23.41 |
| Pyflex [MPA] | 15.20 | 15.85 | 0.65 | 17.10 | 23.72 |
| Deviation design [%] | 3.4 | 3.4 | 1.7 | 3.4 | 3.4 |
| Deviation Nugteren [%] | 1.4 | 1.7 | 5.0 | 1.5 | 1.3 |
| Layer 2 - Layer 3 | |||||
| Design [MPa] | 5.15 | 6.02 | 0.83 | 6.20 | 8.11 |
| Nugteren [MPA] | 6.09 | 6.89 | 0.81 | 7.17 | 9.50 |
| Pyflex [MPA] | 6.11 | 6.94 | 0.83 | 7.21 | 9.54 |
| Deviation design [%] | 18.7 | 15.3 | 0.0 | 16.4 | 17.6 |
| Deviation Nugteren [%] | 0.4 | 0.8 | 2.4 | 0.6 | 0.4 |
| Layer 3 - Layer 4 | |||||
| Design [MPa] | 2.10 | 2.48 | 0.38 | 2.54 | 3.28 |
| Nugteren [MPA] | 2.97 | 3.36 | 0.40 | 3.49 | 4.62 |
| Pyflex [MPA] | 2.90 | 3.30 | 0.40 | 3.43 | 4.53 |
| Deviation design [%] | 38.2 | 33.0 | 4.5 | 34.9 | 38.1 |
| Deviation Nugteren [%] | -2.3 | -1.8 | -0.8 | -1.8 | -2.0 |
Based on this table it is obvious that this model suffers from the same overprediction of contact pressures for the outer layer that the model proposed by Nugteren, as all results are compareble with the results from that model. The small differences stems from Nugteren using an iterative solution taking into account that the area of the outer and inner pressure cahgnes as the pipe expands and contracts and that PyFlex corrects for force equilibrium. The differences are direct results of over predicting the tensions in the outer layer.
The higher contact pressures will make the friction stresses be on the conservative side.
The validation of the bending model suffers from lack of data defining the geometry of the riser in question. In Nugterens thesis (2015) she explains how she found the numbers she has applied. The properties she came up with are also applied in the PyFlex model:
| Property | Layer 1 | Layer 2 | Layer 3 | Layer 4 | unit |
|---|---|---|---|---|---|
| Layer radii | 77.832 | 81.36 | 82 | 93 | mm |
| Layer thickness | 1 | 1 | 5 | 5 | mm |
| Layer width | 2.5 | 30 | 10 | 10 | mm |
| Lay angle | -87.7 | 87.7 | 35 | -36.7 | degrees |
| Number of tendons | 1 | 0 | 38 | 42 | - |
| YoungsModulus | 210 | 210 | 210 | 210 | MPa |
| FrictionFactor | 0.0 | 0.2 | 0.2 | 0.2 | - |
Nugteren only compared the stresses in the third layer, as that is most usually the critical one for fatigue. Also, she applied the bending formulae proposed in the Handbook on Design and Operation of Flexible Pipes (2014), which is the same as Sævik(1992) presented. The PyFlex results are also generated using this model for local bending of the wires. In the validation case a tension of 1000 \(kN\) is applied without any internal or external pressure, while the curvature goes up to 0.3 \(m^{-1}\). The curvature was applied as \(\kappa_2\).In the following table the results are compared:
| \(\theta = 0 deg\) | \(\theta = 45 deg\) | ||||||
|---|---|---|---|---|---|---|---|
| Helica | Nugteren | PyFlex | Helica | Nugteren | PyFlex | ||
| [MPa] | [MPa] | ||||||
| Axial stress | \( \sigma_{11} \) | 326 | 315 | 315 | 320 | 315 | 315 |
| Friction stress | \( \sigma_{fric} \) | 168 | 161 | 161 | 84 | 85 | 114 |
| Bending stress | \( \sigma_{b} \) | 66 | 71 | 71 | 281 | 293 | 293 |
As can be seen the stresses matches very well. Except for the friction stress at 45 degrees. The stresses differ here because we keep an sinusoidal stress distribution, while in Helica and Nugterens model a linear distribution is clearly applied. For computational efficiency it is benificial to keep the same distribution in both the stick and slip regimes, and as the sinusoidal distribution is always on the conservative side, this is choosen.
| Symbol | Description |
|---|---|
| \( \alpha \) | Lay angle |
| \( \epsilon_{11}\) | Axial strain in a tendon |
| \( \epsilon_a \) | Axial strain for pipe |
| \( \kappa \) | Curvature |
| \( \kappa_2 \) | Curvature around axis 2. See Coordinate system and definitions |
| \( \kappa_3 \) | Curvature around axis 3. See Coordinate system and definitions |
| \( \nu \) | Poisson's ratio |
| \( \sigma_{11} \) | Axial stress in a tendon |
| \( \sigma_{b} \) | Bending stress |
| \( \sigma_{fric} \) | Friction stress |
| \( \sigma_{fric,max,i} \) | Maximum stick stress in a tendon in layer i. |
| \( \theta \) | Angle of cross sectional position. See Coordinate system and definitions |
| \( \theta_{rel}\) | Relative angle between tendon and curvature. See Coordinate system and definitions |
| \( A_{tendon} \) | Crossectional area of a tendon |
| \( b \) | Breadth of a tendon |
| \( E \) | Elastic modulus |
| \( f_f \) | Fillfactor |
| \( N \) | Number of layers |
| \( n_{tendons} \) | Number of tendons in a layer |
| \( p_{ext} \) | External pressure |
| \( p_{int} \) | Internal pressure |
| \( p_i \) | Pressure on the inside of a layer |
| \( R_i \) | Mean radius of a layer |
| \( r_{ext} \) | External radius |
| \( R_{inner} \) | Inner radius. Midpoint between two layers. |
| \( r_{int} \) | Internal radius |
| \( R_{outer} \) | Outer radius. Midpoint between two layers. |
| \( t_{eff} \) | Effective tension |
| \( u3 \) | Radial displacement |
Custodio, A., B., Vaz, M.A. A nonlinear formulation for the axisymmetric response of umbilical cables and flexible pipes. Applied Ocean Research 24, 2002
MARINTEK/NTNU/4Subsea Handbook on Design and Operation of Flexible Pipes, 2014.
Nugteren, F.(2015) Flexible Rieser Fatigue Analysis:Studying Conservatism in Flexible Riser Fatigue Analysis and Development of an Engineering Model to Study Influencing Parameters of Local Wire Stress. Delft University of Technology, The Netherlands.
Skeie, G., Sødahl, N. and Steinkjer O. Efficient Fatigue Analysis of Helix Elements in Umbilicals and Flexible Risers: Theory and Applications. Journal of Applied Mathematics, 2012
Sævik, S., On stresses and fatigue in flexible pipes, 1992.
Witz J., Tan Z. On the flexural structural behaviour of flexible pipes, umbilicals and marine cables. Marine Structures, 1992.